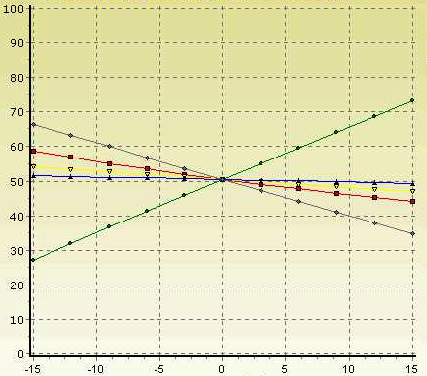
O LINGO inclui um conjunto abrangente de ferramentas de análise para depurar programas lineares, inteiros e não lineares inviáveis, usando técnicas avançadas para isolar a fonte de infalibilidade ao menor subconjunto das restrições originais.
Também possui ferramentas para realizar a análise de sensibilidade para determinar a sensibilidade da base ideal às alterações em determinados componentes de dados (por exemplo, vetor objetivo e valores do tamanho à direita).
No exemplo acima foi usado o modelo da Fabrica de Motores (B01-01) usando a opção SOLVER menu principal em seguida a opção do sub-menu RANGE, para obter o relatório a seguir:

Ranges in which the basis is unchanged:
Faixas de valores para os quais a base fica inalterada. Portanto, temos uma Analise de Validade da solução:
- Coeficientes das variáveis na função objetivo;
- Limites das Restrições.
Objective coefficiente Ranges:
Neste bloco do relatório, serão analisados os coeficientes da Função Objetivo.
Consideremos a linha [ PRODUZIR(( M1100,P2)] , que significa o lucro unitário para produzir o motor de modelo M1100 na Planta P2 temos a informação de que o coeficiente fornecido foi $275 e que ele pode variar entre $275 – $25 = $250 e infinito mantendo-se a mesma solução.
Righthand side Ranges:
Aqui teremos uma analise das restrições, também conhecidos como RHS (Right Hand Side). Na linha 2 o RHS é $1000, assim sendo:
Allowable Increase :
Significa que podemos aumentar o limite em $1000 + $2000 = $3000
Allowable Decrease:
Significa que podemos diminuir o limite em $1000 – $1000 = 0
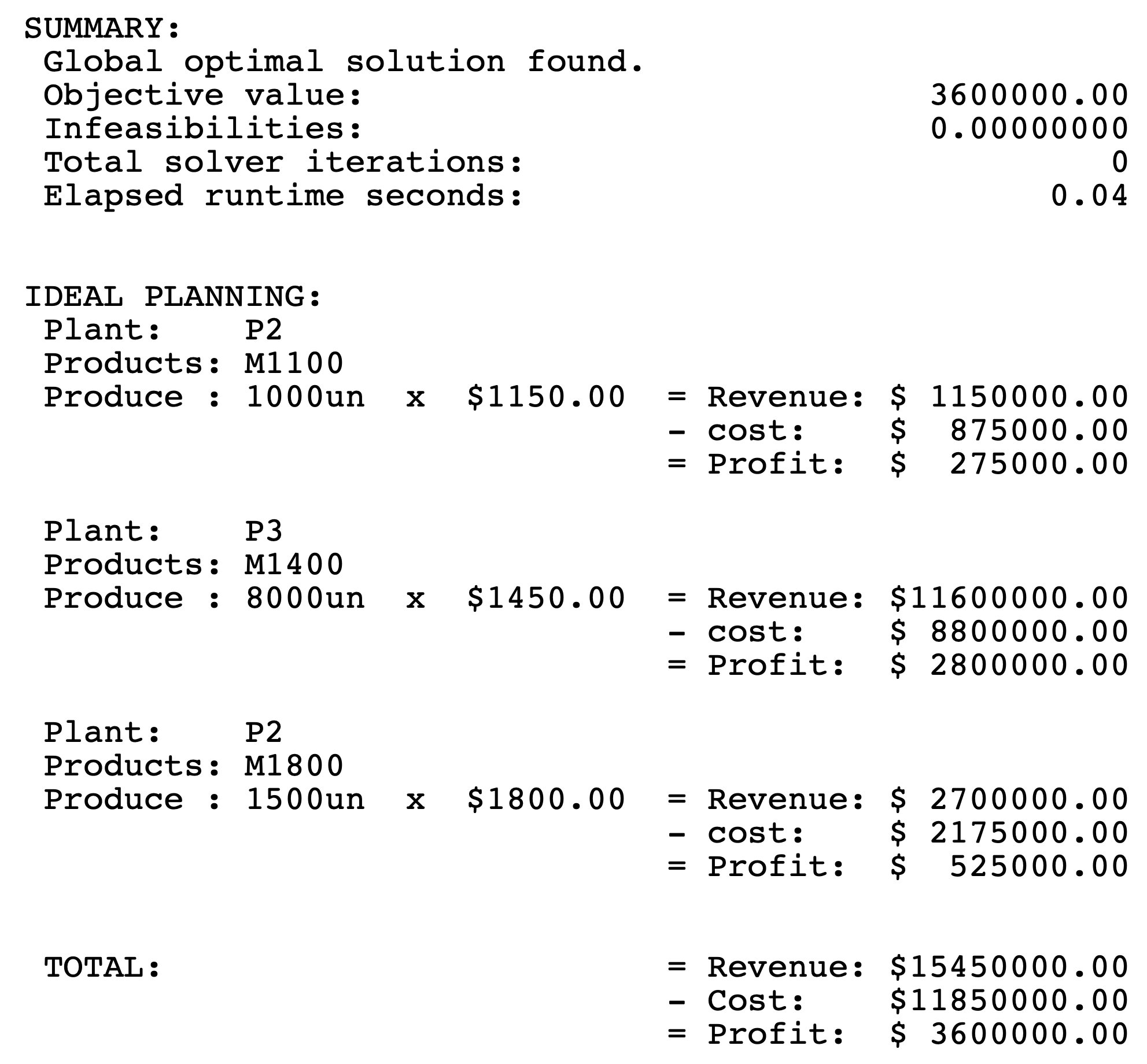
Segue o relatório da solução obtida através do modelo B01-01-RE, para auxiliar na analise:
Esse tema ainda está em fase de elaboração.
