Ilustração de programação Dinâmica (ver Anderson, Sweeney & Williams, uma introdução à Mgr Science, 6ª Ed). Temos uma rede de 10 cidades. Queremos encontrar o comprimento da rota mais curta da cidade 1 para a cidade 10.
ETAPA 1:
Aqui está nosso conjunto primitivo de dez cidades, onde F (i) representa a distância mais curta da rota da cidade i até a última cidade: CITIES / 1..10/: F
ETAPA 2:
O conjunto derivado ROADS lista as estradas que existem entre as cidades (nota: nem todas as cidades.) Os pares são diretamente ligados por uma estrada e as estradas são assumidas de uma maneira.
ETAPA 3:
A seguir, é apresentada a programação de recursão dinâmica. Em outras palavras, a distância mais curta da cidade i à cidade 10 é a mínima em todas as cidades j alcançável a partir da soma da distância de i a j mais a distância mínima de j à cidade 10;
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 1 | 5 | 2 | |||||||
| 2 | 13 | 12 | 11 | |||||||
| 3 | 6 | 10 | 4 | |||||||
| 4 | 12 | 14 | ||||||||
| 5 | 3 | 9 | ||||||||
| 6 | 6 | 5 | ||||||||
| 7 | 8 | 10 | ||||||||
| 8 | 5 | |||||||||
| 9 | 2 | |||||||||
| 10 |
REPORT
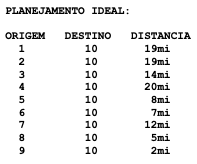
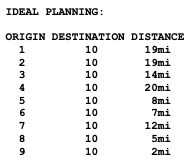
FONTE 6 LINGO the modeling Language and Optimizar Lindo Systems Inc Lindo Systems Inc, 2018



